DENEY-3 : REFRAKTOMETRİ

1.AMAÇ

            Derişimleri bilinen laktoz ve glukoz çözeltilerinden yararlanarak, abbe refraktometresi kullanılarak kırma indisi grafiği oluşturup derişimi bilinmeyen laktoz ve glukoz çözeltilerinin derişimlerinin tayin edilmesi.

2.KURAMSAL BİLGİLER

            Refraktometri, her ortamın kırılma indisinin farklı olması prensibini kullanarak, konsantrasyon ve madde miktarı gibi tayinleri yapmaya yarayan bir yöntemdir. Kırılma indisi her maddeye özgü bir fiziksel özelliktir, bu sebeple kalitatif ve kantitatif analizlerde kullanabileceğimiz bir metoddur. Günümüzde organik bileşiklerin kantitatif analizinde NMR, infrared spektroskopisi gibi yöntemler daha çok tercih edilmektedir.

Bir ortamın kırılma indisine n, elektromanyetik ışımanın vakumdaki hızına c, elektromanyetik ışımanın bu ortamdaki hızına da v dersek, şöyle bir bağıntı elde ederiz:

n = c / v

Benzer maddelerin kırılma indisleri birbirine çok yakın olduğundan ( 1.25 -1.80 arası) ±0.001 duyarlılıkla ölçüm yapabilmemiz gerekir.

Işının bir ortama geliş açısına i, yansıma açısına da r dersek eğer, Snell Yasasına göre şöyle bir bağıntı yazabiliriz:

sini / sinr = v₁ / v₂ = n₁ / n₂

* v₁: Işının 1. ortamdaki hızı
* v₂: Işının 2. ortamdaki hızı
* n₁: 1. ortamın indisi
* n₂: 2. ortamın indisi

Işının geliş açısı, ışının hızı ve ortamın indisi ile orantılıdır. Işının geliş ve yansıma açılarını bilmemiz halinde, iki ortamın kırılma indislerinin oranlarını bulabiliriz. Ya da bir ortamın indisini biliyorsak, diğer ortamın indisini de bu bağıntı sayesinde hesaplayabiliriz.

Kırılma indisleri farklı olan bölgelerde ışının hareketi iki şekilde gerçekleşir:

n₂ > n₁ koşulunda, i geliş açısı, r yansıma açısından daha büyük olacaktır. Geliş açısı büyüdükçe, kırılma açısı da büyür. Buna rağmen geliş açısı, kırılma açısından her zaman daha büyüktür.

n₁ > n₂ koşulunda, yüksek yoğunluklu ortamdan düşük yoğunluklu ortama geçiş sırasında yansıma açısı, geliş açısından daha büyüktür. Geliş açısı büyüdükçe, yansıma açısı da 90º‘ye yaklaşır.

Kritik Açı

Işımanın 90º ’lik bir açı ile kırılmasını sağlayan geliş açısına kritik açı denir. Işının kritik açıdan daha küçük bir değerle gelmesi halinde, yansıma sonucu aydınlık bölge oluşur. Eğer ışın iki ortam arasındaki yüzeye kritik açıdan daha büyük bir açıyla gelirse, ışın kırılmaya değil, yansımaya uğrar. Yoğunluğu büyük ortama kritik açıyla gelen bir ışın, 90ºlik bir açı ile kırılır. Yoğunluğu küçük ortama 90ºlik açı ile gelen bir ışın ise yoğunluğu büyük olan ortama kritik açı ile girer. Snell yasasından yararlanarak şöyle bir bağıntı yazabiliriz:

sin Ө_c=n₂/n₁

Refraktometri cihazının içerisinde prizmalar kullanılır. Gönderdiğimiz ışın örnekten geçip prizmaya değişik açılarla gelir. Eğer geldiği açılar kritik açıdan küçükse, aydınlık bölge oluşur. Kritik açıdan büyük açılarla gelmişse, karanlık bölge oluşur. Karanlık ve aydınlık bölgenin sınırı kritik açıya karşılık gelir. Bir maddenin kırılma indisi, kullanılan ışımanın dalga boyuna, sıcaklığa ve derişime bağlıdır. Bunun dışında sıkıştırılabilen maddelerin kırılma indisi, basınca bağlı olarak da değişir. Dalga boyunun kırılma indisine etki etmesinden dolayı, kullandığımız ışımanın dalga boyunu da belirtmeliyiz. Ticari refraktometrelerde genellikle sodyumun atomunun yaydığı yaklaşık eşit şiddetlerdeki, 589.0 ve 589.6 nm ‘deki hatları kullanılır. Bu hatlar sodyum D hatları olarak adlandırılır.

Abbe Refraktometresi

            Kırılma indisi tayininde kullandığımız alete Abbe Refraktometresi denir. Abbe refraktometresinde iki prizmanın arasına kırılma indisini tayin edeceğimiz maddeyi sıvı film olarak yerleştiririz. Prizmalara gönderdiğimiz ışık ile, kritik açıdan daha küçük açı ile gelen ışınların oluşturduğu aydınlık bölge ve kritik açıdan daha büyük açıyla gelen ışınların oluşturduğu aydınlık bölgeyi görebiliriz.

Nicel Analiz: Ölçtüğümüz kırılma indisi değerlerini, saf maddelerinin kırılma indisi değerleri ile karşılaştırarak refraktometrik nicel analizi gerçekleştirmiş oluruz. Eğer karşılaştırma yapacağımız standart bir indis değeri bulamazsak, Lorentz-Lorenz molar kırılma indisini buluruz. Bu değer R ile gösterilir ve

R=(n²-1)xM/(n²+2) x d ile de formülize edilebilir.

M, molekülün molar ağırlığı, d ise yoğunluğudur. Buradan R değerini buluruz ve bilinen değerler ile hesapladığımız R´ değeriyle karşılaştırma yaparız.

                           

Kırılma İndisi

Işığın boşluktaki yayılma hızının made içindeki yayılma hızına oranına kırılma indisi, denir.

Refraktometreler “Kritik Işın” ve kritik açının sağladığı olanaklardan yararlanılarak yapılmıştır. Normalle ( yaklaşık 90°) açı yaparak yani yüzeye paralel olarak gelen ışın ile  artık kırılma açısından daha büyük açıda kırınan ışın elde edilemiyorsa bu ışına kritik ışın, açıya da kritik açı adı verilir.  Işının çıktığı yüzeyden örneğe bakıldığında yüzeyin bir kısmı karanlık, bir kısmı  aydınlık görülür. Bu bölgelerin büyüklüğü kırılma açısının büyüklüğü ile ilgilidir.

                             İşte refraktometreler bu temle ilkeye dayanır.

Kırılma indisini sıcaklık, ışığın dalga boyu ve  basınç etkiler. Ortamın soğurma yapmadığı dalga boyunda dalga boyu değeri atttıkça kırılma indisi azalır.

Ortamın soğurma yaptığı dalga boyu yakınlarında ise dalga boyu değeri arttıkça kırılma indisi artar.Kırılma indisi ölçümü genelde çoğu kez sodyumun D yayım çizgisinde yapılır.Kırılma indisinin ölçüldüğü ışın alt indis ve ortamın sıcaklığı üst indis olacak şekildeyazılır. n_D²⁰ gibi.     

Kırılma İndisi Ölçümünün Kullanıldığı Yerler

Kırılma indisi  E.N ve K.N. gibi bir kimyasal türün belirlenmesinde kullanılan sabitlerdendir.
Endüstride saflık kontrolünde kullanılır. Kırılma indisleri ile derişim arasındaki ilişkiden derişim tayini yapılabilir. Şeker tayininde, camda SiO₂ tayininde ve  petrolde aromatik hidrokarbonların analizinde de kırılma indisinden faydalanılmaktadır.

3.KULLANILAN MALZEMELER

• Abbe Refraktometresi
• Damlalık
• Beher
• Çeşitli konsantrasyonlarda hazırlanmış glukoz çözeltisi (%1, %2, %3, %4, %5)
• Çeşitli konsantrasyonlarda hazırlanmış laktoz çözeltisi (%1, %2, %3, %4, %5 )

4.DENEYİN YAPILIŞI

 Deneye başlamadan önce cihazımızın kalibrasyonunu gerçekleştirdik. Kalibrasyon işlemini saf su ile yaptık çünkü kullanmış olduğumuz çözücü sudur. Daha sonra  %1, %2, %3, %4, %5 lik glukoz çözeltilerinden  abbe refraktometresine sırayla %1 lik glukoz çözeltisinden birkaç  damla prizma üzerine damlatıldı ve diğer prizma kapatıldı. Yayılan glukoz çözeltisi mercekten bakıldı karanlık ve aydınlık bölgeler görüldü. Karanlık ve aydınlık bölgeyi ayıran saç teli çarpı işaretinin tam ortasına getirilince okuma tuşuna basılarak kırma indisi okundu. Daha sonra %2 lik çözeltinin kırma indisini ölçmeden önce prizmalar etanol ile iyice silindi ve %2lik çözeltiden 2 damla prizma üzerine damlatılarak ölçüm yapıldı. Bu işlem diğer çözeltiler içinde tekrarlanarak kırma indisleri kaydedildi. Aynı işlem laktoz çözeltisi içinde yapıldı.

5.Veriler ve hesaplamalar

Tablo.1:Glukoz çözeltilerinin kırma indisleri değerleri

Glikoz çözeltilerinin derişimleri	Kırma indisleri
%0	1,3334
%1	1,3340
%2	1,3348
%3	1,3363
%4	1,3370
%5	1,3403
Bilinmeyen çözelti	1,3370

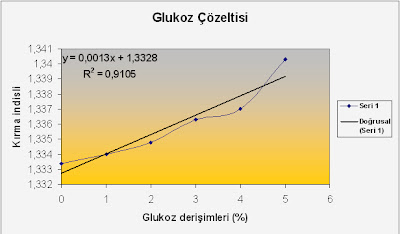
Grafik.1:Glukoz derişimlerine karşı kırma indisleri grafiği

Grafikten yararlanılarak denklem bulunur ve bu denklemde konsantrasyonu bilinmeyen glukoz çözeltisinin konsantrasyonu  tayin edilmiş olunur. Bilinmeyen glukoz çözeltimizin kırma indisi 1,3370 olarak cihazımızda okunmuştu.

y=0,0013x + 1,3328

1,3370 = 0,0013x +1,3328

X = %3,231 bilinmeyen glukoz çözeltisinin yüzde derişimi

Tablo.2:Laktoz çözeltileri derişimleri ve kırma indisi değerleri

Laktoz çözeltileri derişimleri	Kırma indisi
0	1,3334
%1	1,3354
%2	1,3364
%3	1,3377
%4	1,3391
%5	1,3404
Bilinmeyen çözelti için	-

Grafik.2:Laktoz çözeltisi derişimlerine karşı kırma indisleri değerleri

Grafikten yararlanılarak denklem bulunur ve bu denklemde konsantrasyonu bilinmeyen laktoz çözeltisinin konsantrasyonu tayin edilebilir.  

DENEY-2 GÖRÜNÜR BÖLGE (visible) SPEKTROSKOPİSİ

ÖZET

Bu deneyde UV-Visible spektrofotometresinin kullanımı ve çalışma prensibi hakkında bilgi edinmiş olduk. Uv-visible bölge absorpsiyonları moleküler absorpsiyon spektrometrisi içerisinde yer alır. 340-750 nm dalga boyu aralığında duyarlılığa sahip bir yöntemdir. Genellikle organik ve inorganik bileşiklerin kantitatif analizinde yaygın olarak kullanılır.

Yapmış olduğumuz deneyde farklı konsantrasyonlarda amonyum fosfa molbdat çözeltileri alarak UV-Visible spektrofotometrisinde absorbantları ölçüldü ve konsatrasyona karşı absorbans grafiği çizildi. Bunun sonucunda konsantrasyonu bilinmeyen bir amonyum fosfa molbdat çözeltisinin konsantrasyonunu tayin etmiş olduk.

1.AMAÇ

     Lambert-Beer Kanunu doğrulayan uv-visible spektrofotometresiyle fosfat tayinini yapılmasıdır.

DİKKAT: kare şeklindeki kutucuklar içerisinde  işareti vardır. 

2.TEORİK BİLGİ

2.1. TEMEL KAVRAMLAR

Monokromatik ve I₀ şiddetindeki bir ışık demeti, kalınlığı b cm olan bir tüpte bulunan çözeltideki herhangi bir molekül tarafından absorplandığında şiddeti azalır ve tüpü I, şiddetinde terk eder. Işımanın şiddetindeki bu azalmanın bir kısmı örnek kabının çeperlerinde ortaya çıkan yansımalar veya çözeltide bulunabilecek asılı taneciklerinin yol açtığı saçılmalar sonucu oluşur. Sadece moleküllerin o dalga boyundaki ışımaya absorplaması sonucu ortaya çıkan azalma BEER-LAMBERT eşitliği ile verilir. Bu eşitliğe göre, örnek kabına giren ve kabı terk eden ışık şiddetlerinin logaritmalarının farkı, ışıkla etkileşen moleküllerin birim hacimdeki sayısı ile yani derişim ile orantılıdır:

Log (Io/I)= bc=A                                    (1)

A ile C arasında bu basit doğrusal ilişkiden analitik uygulamalarda yararlanılır. Eşitlikte derişim C, mol/L, örnek kabının kalınlığı b ise cm birimindedir, , molar sönüm veya molar absorpsiyon katsayısı ya da molar absorptivite olup, birimi L/mol.cm dir; A ise absorbans adını alır.A’ya optik yoğunluk veya sönüm adları verilir. Derişimin g/L olarak kullanılması halinde A’yı C’ye bağlayan eşitlikte katsayı a ile gösterilir ve birimi L/g.cm olarak verilir; a, sönüm veya absorpsiyon katsayısı ya da absorptivite adını alır:

A = abc

Örnek kabını terk eden ve kaba giren ışık şiddetleri arasındaki orana geçirgenlik, T, adı verilir:

I/I_o= T =10^-bc                     (2)

Görüldüğü gibi, geçirgenlik ile derişim arasındaki ilişki üstel olup bunun uygulamada

kullanılması zordur. A ile T arasındaki basit ilişki ise,

A= -logT = 2- log %T                        (3)

şeklindedir ve % T, yüzde geçirgenlik adını alır.

Normal olarak geçirgenlik ve absorbans ölçümlerinde,analit çözelti geçirgen bir kapveya hücrede bulunması gerektiği için laboratuvarda ölçülemezler.İki hava/kap ve iki kap/çözelti ara yüzeylerinde yansımalar olur. Ayrıca ışın şiddetinde,büyük moleküllerin ışını saçmaları ve bazen kap yüzeyinin absorpsiyonu nedeniyle de azalma olabilir.Bu etkileri düzeltmek için analit çözeltiden geçen ışın gücü,genellikle içinde yalnız çözücü bulunan eşlenik bir hücreden geçen ışın gücü ile kıyaslanır.Gerçek geçirgenlik ve absorbansa çok yakın deneysel geçirgenlik ve absorbans değerleri bu eşitlikten bulunur:

T=(P_çözelti/P_çözücü)=P/P₀

Çözeltide, uygulanan dalga boyundaki ışığı absorplayacak birden fazla molekülvarsa, A toplamsal bir değer olduğundan.

A=A1+A2+..............=₁bc₁ + ₂bc₂                                         (4)

eşitliği geçerlidir.

2.2. BEER YASASI

Aşağıdaki şekilde olduğu gibi absorplayıcı bir madde bloku (katı, sıvı veya gaz) düşünelim. P₀ gücünde paralel monokromatik bir ışın demeti blok yüzeyine dik olarak düşsün; N tane absorplayıcı atom, iyon veya molekül içeren b uzunluğundaki maddeden geçerken absorpsiyon sonucu ışın gücü P değerine düşer. Blokun son derece düşük dx kalınlığındaki S kesit alanını göz önüne alalım. Bu kesit alanda dn tane absorplayıcı tanecik bulunur; her bir tanecikte foton yakalanmasının gerçekleştiği bir yüzeyin varlığı düşünülebilir. Eğer foton bu yüzeylerden birisine ulaşırsa, hemen yakalanır. İlgili kesit alandaki yakalayıcı yüzeyin toplam alanı dS ile gösterilir; böylece foton yakalayıcı yüzeyin toplam yüzey alanına oranı dS / S olur. İstatistik ortalamaya göre, bu oran ilgili kesitte fotonun yakalanma olasılığını gösterir.

P_o başlangıç gücündeki bir ışının gücünün, litrede c mol absorplayıcı madde içeren b cm ışın, yoluna sahip bir çözelti tarafından azaltılması. P < P_o

İlgili kesitte giren ışının şiddeti P_x , 1cm² deki foton sayısı ile orantılıdır ve dP_x bu kesitte absorplanan miktarı gösterir; böylece absorplanma kesri –dP_x / P_x olur ve bu oran fotonun yakalanmasının ortalama olasılığını verir. P nin azaldığını göstermek için terime eksi işareti verilir. Böylece

-dPx / Px = dS / S

dS’ nin taneciklerin foton yakalayıcı yüzeylerinin toplam alanı olduğunu hatırlayalım; bu nedenle dS toplam tanecik sayısı ile orantılı olmalıdır, veya

dS = adn

olur. Bu eşitlikte dn tanecik sayısı ve a yakalama kesit alanı olaraktan adlandırılabilecek bir orantı sabitidir. 0 ve n aralığında integrali alınırsa;

-∫ dP_x / P_x = ∫ adn / S

elde edilir ve integral çözülünce,

-ln ( P / P0 ) = an / S   bulunur.

Kesit alanı S blokunun cm³ olarak hacmi V ve cm olarak uzunluğu b cinsinden

verilebilir. Böylece S = V / b cm² olur. Eşitlik düzenlenirse;

log ( P0 / P ) = anb / 2.303V   elde edilir.

n / V nin biriminin derişim birimi yani, 1cm³ teki tanecik sayısı olduğuna dikkat

edersek, n / V değerini litrede mol olarak verebiliriz.

Böylece mol sayısı;

mol sayısı = n tanecik / ( 6.02*1023 tanecik/mol ) olarak verilir ve c, mol / litre

cinsinden

c = ( 1000n / 6.02*1023V ) mol / litre    eşitlikler birleştirilince;

log ( P0 / P ) = 6.02*1023abc / 2.33*1000  elde edilir.

Son olarak bu eşitlikteki sabit değerle tek bir terim olan ε’ da toplanabilir.

log ( P0 / P ) = εbc = A

bu ise Beer Yasasının formülle gösterimidir.

2.3. Beer Yasasının Karışımlara Uygulanması

Beer Yasası birde çok absorplayıcı madde içeren karışımlar içinde geçerlidir. Türlerin birbirlerini etkilememesi koşuluyla, çok bileşenli bir sistemin toplam absorbansı

A_toplam = A₁ + A₂ + .... + An = ₁bc₁ + ₂bc₂ + ... + _nbc_n

olarak verilir.

Beer-Lambert eşitliğinin geçerli olabilmesi için uygulanan ışığın gerçekten

monokromatik yani tek dalga boyu değerinde olması, absorpsiyon olayının örneğin her yerinde eşit miktarda olması yani,örneğin homojen olması,ayrıca birden fazla bileşenin ışığı absorplaması halinde,her bir bileşenin, diğerlerinin absorpsiyonunu etkilememesi gerekir. Bu koşulların sağlanması halinde, A ile C arasındaki ilişki doğrusaldır.Genellikle C değerinin, 0.01 M dan daha küçük olduğu durumlarda bu doğrusallık sağlanır. Daha derişik çözeltilerde, moleküller arası etkileşmeler önem kazanır ve bu etkileşmeler A ile C arasındaki doğrusal ilişkinin bozulmasına neden olur. A ile C arasındaki bağıntıda orantı katsayısı aslında  değil, n/(n²+2)² dir ve ancak seyreltik çözeltilerde n/(n²+2)² değerinin derişimle değişimi ihmal edilebilir. Derişim arttıkça çözelitinin kırılma indisi, n, artar ve n/(n²+2)² değeri azalır. Bu etki nedeniyle derişik çözeltilerde A ile C arasındaki doğrusal ilişkiden negatif yönde sapmalar ortaya çıkar.

Beer-Lambert eşitliğinde sapmalara yol açabilecek bir başka faktör ise,örneğe gönderilen ışığın tam monokromatik olmaması veya örneğin ışık kaynağından gelen ışığa ek olarak dışarıdan kaçak ışığın gelmesidir.Bunu daha kolay anlayabilmek için örneğe iki ayrı dalga boyunda I_o ve I_o şiddetlerindeki ışığın geldiğini ve örneğin bu ışınları absorpladığını düşünelim. Bu durumda,

eşitliği geçerli olur. Eşitlikten görüldüğü gibi,örnek her iki dalga boyundaki ışımayı aynı miktarda absorpluyorsa, yani =’ ise ,eşitlik tek dalga boyundaki eşitliğe indirgenir ve bu nedenle doğrusallıktan bir sapma gözlenmez.  büyüktür ’ ise ölçülen A, tek dalga boyu için ölçülmesi gereken değerden daha küçük olur ve doğrusal ilişkiden negatif bir sapma ortaya çıkar.  küçüktür ’ olması durumunda ise bu sapma pozitiftir.

Bir spektrofotometrede ışık kaynağından çıkan polikromatik, yani çok dalga boylu ışık demetinden monokromatör adı verilen düzenek yardımı ile monokromatik, yani tek dalga boylu ışık seçilir ve bu ışık ince bir aralıktan geçirilerek örneğe gönderilir. Işık ne kadar dar bir aralıktan geçirilirse istenilen dalga boyundaki ışık o kadar saf olarak elde edilir. Aralığın fazla açılması halinde istenilen dalga boyu ile beraber buna yakın değerlerdeki dalga boyları da örneğe gönderilmiş olur.Örneğe gönderilen ışık,geniş bir dalga boyu aralığı içeriyorsa,dalga boyu aralığının kenarlarındaki kısmı,merkezdeki kısmından daha az absorbans değerlerinin ölçülmesine neden olur. Böylece,Beer-Lambert eşitliğinden negatif sapmalar ortaya çıkar. İncelenen örnekte disosyasyon, asosyasyon, polimerleşme, kompleks oluşumu gibi dengelerin oluşması ile de Beer-Lambert eşitliğinden sapmalar ortaya çıkar. Örneğin, benzoik asidin sulu çözeltisinde,

disosyasyon dengesi kurulur. Burada asidin ışığı absorplama dalga boyu maksimumu, 273 nm, molar sönüm katsayısı 970 dir. İyonlaşmış tür ise maksimum dalga boyu 268 nm ve molar sönüm katsayısı 560 değerlerine sahiptir. Seyrelme ve/veya pH’ın artması ile denge sağa kayacağından, 273 nm deki etkin molar sönüm katsayısı azalır ve beklenenden daha küçük absorbans değerleri ölçülür.

dengesinde de Cr₂O₇^2- ve CrO₄^2- türlerinin ışığı absorpladığı maksimum dalga boyu değerleri farklıdır.Sistem sadece CrO₄^2- nin bulunduğu kuvvetli bazik veya sadece Cr₂O₇^2- nin bulunduğu kuvvetli asidik çözeltide inceleniyorsa,absorbans-derişim ilişkisinde doğrusallık gözlenir.Sistem her iki türü de içeriyor ve pH’ın tamponlamadığı bir çözeltide inceleniyorsa, Beer-Lambert eşitliğinden sapmalar olur.

Bir dengede ışığı absorplayan türlerin ışığı absorplama miktarlarının eşit olduğu bir dalga boyu da bulunabilir.Bu dalga boyuna isosbestik nokta adı verilir. Ölçümlerin bu dalga boyunda yapılması ile, dengede bir türden diğerine geçiş olsa bile, Beer-Lambert doğrusal ilişkisi elde edilir.İncelenen maddenin floresans özelliğine sahip olması, aynen kaçak ışık gibi etki yapar. Ölçüm sırasında ışığı absorplayan türün fotokimyasal bir tepkimeye girerek bozunması da istenmeyen bir durumdur. Her iki olay da A ile C arasındaki doğrusal ilişkiden negatif sapmalara neden olur. Maddenin incelendiği çözücünün değiştirilmesi ile hem absorbans değeri hem de maksimum dalga boyu değeri değişir. Sıcaklık değişmeleri de ölçümlerde hatalara neden olabilir.

Ölçülen absorbans, A,değerlerinin dalga boyuna karşı grafiğe geçirilmesi ile söz konusu maddenin absorpsiyon spektrumu elde edilir. Ölçümlerde elde edilen logA veya %T değerleri de dalga boyuna karşı grafiğe geçirilebilir. Şekil 1 de, bu üç tür absorpsiyon spektrumu için örnekler görülmektedir.

Beer-Lambert eşitliğine göre, A-C doğrusal ilişkisinin sağlanması için, absorbansın dalga boyu değerlerindeki küçük değişmelerden pek fazla etkilenmediği bir dalga boyunun seçilmesi gerekir. Bu da ölçümlerin absorpsiyon spektrumundaki maksimum dalga boyu değerlerinde yapılması ile sağlanır.

Absorpsiyon ölçümleri sırasında karşılaşılan bir başka güçlük ise, incelenen örneğin

geçirgenliğinin çok az veya çok fazla olduğu zaman ortaya çıkar. Geçirgenlik ile derişim arasındaki ilişki logaritmik olduğundan, T’ nin ölçümünde yapılacak bir hata (ΔT) hesaplanan C değerlerinde oldukça büyük bağıl hataya neden olur.

ΔC/C=(0.434/TlogT)ΔT                  (6)

Eşitliği ile hesaplanacak bu hata,görüldüğü gibi ayrıca ölçülen T değerine de bağlıdır.ΔC/C nin T’ye karşı grafiğinin incelenmesi,Şekil 2 de görüldüğü gibi, uygulamada ölçümlerin T=0.2-0.7 arasında yapılması ile bağıl hatanın en aza indirilmesi mümkün olduğunu göstermektedir. Bağıl hatanın en az olduğu T değeri ise 0.368 dir.

3.KULLANILAN MALZEMELER

• Beher
• Spektrofotometre
• Amonyum molibdat çözeltisi
• Sülfürik asid çözeltisi
• Askorbik asid çözeltisi
• Potasyum antimuan tartarat çözeltisi

4.DENEYİN YAPILIŞI

Askorbik Asit Metodu

Askorbik asit metodunda, amonyum molibdat ve antimonil tartarik asit ortamda ortofosfatla reaksiyona girerek heteropoli asit-fosfomolibdik asit teşkil ederler. Bu asit daha sonra askorbik asit ile indirgenerek molibden mavisi rengine sahip bir bileşiğe dönüştürülür. Elimizdeki 1000 ppm lik stok çözeltiden 0,2; 0,4; 0,6; 0,8; ve 1 ppm lik çözeltiler hazırlamak mümkün olmadığından dolayı önce bir ara stok çözelti hazırlanır. Stok çözeltiden 10 ml balon joje içerisine alınır. Piset yardımıyla 100 ml saf su ile tamamlanır. Bunun sonucunda 100 ml’lik  100 ppm lik stok çözelti hazırlanmış olur. Hazırlanan stok çözelti 100 ml’lik behere alınarak standart çözeltilerin hazırlanmasına başlanır ve 0,2 mg/L çözelti elde etmek için stok çözeltisinden 200 mikrolitre balon joje içerisine otomatik pipet yardımıyla aktarılarak saf su ile 100 ml’ye tamamlanır ve 0,2 ppm lik 1. standart çözelti elde edilir. Daha sonra stok çözeltiden alınan miktarlar sırası ile 400; 600; 800; 1000 mikrolitre olarak ayarlanır ve 100 ml’ye saf su ile tamamlanarak diğer 4 adet standart çözelti elde edilmiş olur.

Sırası ile 10 ml amonyum molibdat çözeltisinden, 25 ml sülfürik asit çözeltisinden, 10 ml askorbik asit çözeltisinden ve 5 ml potasyum antimuan tartarat çözeltisinden bir beher içerisine alınır ve toplam 50 ml’lik reaktif elde edilir. Beher yavaşça çalkalanırsa hafif sarımsı bir renk oluştuğu gözlemlenir.

Hazırlanan reaktiften her standart çözeltiye 5’er ml eklenir.100 ml saf su bir behere alınarak üzerine reaktiften 5ml eklenir ve bu çözelti kör çözelti olarak adlandırılır. Sonrasında bilinmeyen çözelti hazırlanması için her standart çözeltiden az miktarlarda alınarak bilinmeyen çözelti elde edilir.

Spektrofotometrede dalga boyu 690 nm olarak ayarlanır. Spektrofotometre küveti içerisine kör çözeltiden konularak küvet cihaza yerleştirilir ve cihaz sıfırlanır. Daha sonra tüm standart çözeltilerden küvet çizgisine kadar küvete eklenerek tüm çözeltilerin absorbans miktarları spektrofotometreden okunarak deney sonlandırılır. Okunan absorbans miktarları ve bunlara karşılık gelen konsantrasyon miktarları aşağıdaki tabloda verilmiştir.

5.SONUÇLAR

Tablo 1 : Konsantrasyon-Absorbans Değerleri

Konsantrasyon	Absorbans
0	0
0,2	0,036
0,4	0,085
0,6	0,103
0,8	0,131
1	0,156

6.GRAFİKLER

Grafik  1: Konsantrasyona karşılık gelen absorbans değerleri

Bilinmeyen çözelti için grafiğin denklem formülü kullanılır. Yani;

                        y = 0,1654x

bu formülde absorbansını (0,073 abs) bildiğimiz çözeltinin konsantrasyonunu bulabiliriz.

                        0,073 = 0,1654x

                        x = 0,44 ppm (bilinmeyen çözeltinin konsantrasyonu)

DENEY-1: UV-VIS SPEKTROFOTOMETRE

ÖZET:

Bilinmeyen bir maddenin UV sahasındaki spektrumunun elde edilmesi ve bunun bilinen standartlarla karşılaştırılması ile o maddenin tanımlanması yapılabilir. (Şekil 13)

(Şekil 13); UV- Spektromu

Konsantrasyona karşı okunan, absorbans değerleri bir grafik kağıdı üzerinde noktalanarak birleştirilirse, o maddenin spektrumu elde edir. Elde edilen spektrum, bilinen madde spektrumu ile karşılaştırılır. Karşılaştırma, spektrumun şu özelliklerine göre yapılır:

a) UV sahasında elde edilen max. absorbsiyonu gösteren dalga uzunluğu her madde için karakteristikdir (Max. X).

b) Molar ekstinksiyon katsayısı (A) aynı şartlarda, her madde için sabit ve karakteristik bir değer taşır.

c) Minumum (Min) absorbsiyonu gösteren dalga uzunluğu da bir değerlendirmede yardımcı olur.

Biz bu deneyimizde konsantrasyonu biline bir salisilik asid çözeltisinden farklı konsatrasyonlarda hazırlayarak uv-spektrofotometresinde farklı konsantrasyondaki çözeltilerden bir absorbans konsantrasyon grafiği elde edecez ve bu grafik yardımıyla konsantrasyonu bilinmeyen bir salisilik asid çözeltisinin konsantrasyonunun tayin edeceğiz.

1.AMAÇ:

Konsantrasyonu bilinen bir salisilik asid çözeltisinden farklı konsantrasyonlarda çözelti hazırlayarak bir absorbans-konsantrasyon kalibrasyon eğrisi çizilir ve bu kalibrasyon eğrisi ile konsantrasyonu bilinmeyen bir salisilik asid çözeltisinin konsantrasyonunun tayin edilmesi.





2. TEORİ:




2.1.)ULTRAVİOLET

Ultraviolet ( morötesi ) ışınları elektromanyetik spektrumda X-Ray ile Görünür Bölge arasında yer alır. UV ışınlarının dalga boyları 100 ile 400 nm aralığındadır.
UV ışınlarının soğurulması maddede elekronik geçişlere sebep olur. (elektronik geçiş: Elektronların düşük enerjili temel hal orbitallerinden yüksek enerjili uyarılmış hal orbitallerine geçmesidir.) Soğurulan bu enerji daha sonra ısı, ışın, kimyasal tepkime olarak geri verilir.


2.2.) UV spektrofotometresi:

Ultraviyole spektrofotometre, kimyasal maddelerin UV (200 -380 nm) alanındaki spektrum analizleri için kullanılır. Işık kaynağı olarak, yüksek baskı altındaki hidrojen veya deuterium deşarj lambası (200-375 nm arasında ışın verir) kullanılır.

Genellikle UV spektrofotometreler görünür bölge ile birleşik haldedir ve UV-visible olarak adlandırılırlar. Bu tür spektrofotometreler dalga boyları 100 ile 800 nm arasında değişen ışınlarla tarama yapar. UV ve Görünür Bölge ışık kaynakları aynı sistem içinde kullanılır. Software sayesinde 100 - 400 nm arasında UV ,400 - 800 nm arasında Görünür Bölge ışık kaynağı kullanılır. Ayrıca UV-Visible spektrofotometrelerde derişimleri arasında ölçüm yapılmaktadır. Bu sistemde ışık kaynağından çıkan ışık önce slitten geçerek ışık bölücüye kadar gelir. Burada ışık iki eşit parçaya bölünerek uygun optik sistem yardımıyla referans ve örnek küvetine ayrı ayrı gönderilirler. Küvetlerden çıkan ışık dedektörlere gelir ve burada bu ışık şiddetleri ölçülür ve kaydedilir. Daha sonra elde edilen datalar Absorbansa karşı dalga boyu grafiğine geçirilir ve gerekli hesaplamalar grafik yardımı ile yapılır.



2.3.) UV ve Görünür Bölge Absorpsiyon Spektrofotometreleri

Spektrofotometri renkli maddelerin, bir ayraçla renklendirilen maddelerin ve bazı renksiz maddelerin soğurduğu ışık şiddetini ölçerek yapılan bir analizdir.
Spektrofotmetrelerde dalga boyu analiz yöntemidir. Değiştirilerek dalga boyuna karşı absorbans veya transmitans ölçümü alınır.

Basit Bir Spektrofotometrenin Elemanları

Işık kaynakları:UV ve görünür bölgede D2, W, H2 ve Xe gibi sürekli ışık kaynakları kullanılır.
Monokromatör: (Dalgaboyu Seçicileri) Işık kaynağından gelen polikromatik ışıktan (birden fazla dalgaboyundaki ışık), monokromatik ışık (tek bir dalgaboyunda olan ışık) elde etmek için kullanılan düzenektir. UV ve görünür bölgede prizmalar veya optik ağ adını alan parçalar kullanılır.
Örnek kabı: Eğer 200 ile 320 nm arasındaki bir dalgaboyunda çalışılacaksa örnek kabının kuartzdan yapılmış olması gereklidir. Çünkü bu dalgaboyu aralığında kuartz, ultraviyole ışığı geçirebilir. 320-700 nm arasında bir bölgede çalışılacaksa, örnek kabının camdan yapılmış olması yeterlidir.
Dedektör: Örneğin ışığı absorplayıp absorplamadığını anlamak için, ışık kaynağından gelen ışığın şiddeti dedektör ile ölçülür. UV ve görünür bölgede fotovoltaik veya fotoiletken dedektörler, fototüpler ve fotoçoğaltıcı tüpler dedektör olarak kullanılmaktadırlar.
Spektrofotometrelerde bu ana bileşenlerden başka ışığı toplamak, yansıtmak, bölmek amacıyla mercekler, aynalar, ışık bölücüleri de kullanılır.
Bir bileşiğin hangi dalga boyunda absorbsiyon yaptığını bulmak için absorbsiyon eğrisini saptamak gerekir. Bunun için sözkonusu bileşiğin değişik dalga boylarındaki uygun aralıklarla absorbsiyonu y eksenine , dalga boyu ise x eksenine işaretlenerek bir eğri elde edilir. Bu eğriye absorbans eğrisi denir. Kantitatif ölçümlerde λ max ölçüm için kullanılır. λ max değerinin dışında bir dalga boyunda çalışılması absorbsiyonun az olmasına yol açar.
Aşağıdaki absorbans eğrisinden de anlaşılacağı gibi λ max değerinde maksimum absorbans elde edileceği görülür. Absorbans eğrisinin sağında veya solunda λ değerlerindeki oynamanın, λ max değeri yakınlarındaki oynamalardan daha çok absorbansa yansıyacağı grafik üzerinde görülmektedir.

Her bir renkli sıvı, normal ışığı oluşturan ışıklardan bir yada birkaçını absorblar. Öbürlerini de az yada hiç absorblamaz, olduğu gibi geçirir. Buna göre kırmızı bir çözeltiyi ölçmek için spektrofotometride kulanılacak

ışık, yeşil bir ışık olmalıdır. (komplementer renkler)

Dalga Boyu                             Bölge                  Gözle Görünen Renk

<380                           UV                   Görünmez

380-440                        Görünür                      Mor

440-500                        Görünür                     Mavi

 500-580                      Görünür                        Yeşil

580-600                      Görünür                          Sarı

600-620                       Görünür                   Turuncu

620-750                       Görünür                      Kırmızı

750-2000                          IR                       Görünmez

İnsan gözünün yanıt verdiği ışınsal enerji 400-750 nm arasındaki bölgeyi kapsar.
Bu ışınların ölçümleri insan gözüyle değilde spektroskopik yöntemlerle yapıldığında daha hassas sonuçlar elde edilir. Bunun içinde Lambert-Beer yasasından faydalanılır.

2.4.) Lambert- Beer Yasas
Maddenin ışığı soğurma (absorplama) derecesini ölçmek ve bundan yararlanarak derişimi saptamak için, soğurma ile derişim arasındaki ilişki bilinmelidir. Monokromatik (tek dalgaboylu ışıma) ve Io şiddetindeki bir ışık demeti, kalınlığı b cm olan bir tüpte bulunan çözeltideki herhangi bir molekül tarafından absorplandığında şiddeti azalır ve tüpü I şiddetinde terkeder. Moleküllerin seçilen dalgaboyundaki ışımayı absorplaması sonucu ortaya çıkan azalma Beer- Lambert eşitliği ile verilir
Renkli bir çözeltiye giren ışığın şiddeti I0, çözeltiden çıkan ışığın şiddeti I ise I’nın Io’ oranına geçirgenlik veya transmisyon denir ve “T” ile gösterilir. Transmitans ile absorbans

A = - log T = log I / T = log 100 / %T

A = log 100 - log %T

A = 2 - log %T

A = log( I0/I)

Absorbans; giren ışın şiddetinin çıkan ışığın şiddetine oranının logaritmasıdır.
Yasa A = εbc şeklinde ifade edilir. ε, Molar soğurma katsayısı,b örnek kalınlığı ve c ise derişimi ifade eder.
Bir çözeltinin transmitansı ve absorbansı; ışığın geçtiği yolun kalınlığına (küvet kalınlığı), çözeltinin konsatrasyonuna ve her bileşik için sabit olan molar soğurma katsayısına bağlıdır.
Beer- Lambert eşitliğinin geçerli olması için; uygulanan ışık monokromatik olmalıdır, örnek homojen olmalıdır ( absorpsiyonun örneğin her yerinde eşit olması) ve birden fazla bileşen varsa, her bir bileşen diğerlerinin absorpsiyonunu etkilememelidir

2.5.) Lambert-Beer Yasasından Sapmalar

Derişim Etkisi: 10-2 M dan daha derişik çözeltilerde sapma olur. Nedeni artan tanecik sayısı nedeniyle taneciklerin etkileşimleri artar ve molar soğurma katsayısını değiştirirler. Ortamdaki soğurum yapmayan türler fazla ise de sapma olur. Kırılma indisi derişimle artar. Ancak bu düzeltilebilr. 10-2 M dan daha derişik çözeltilerde kırılma indisi önemsizdir.

Kimyasal Sebepler: Soğurma yapan türün derişimi kimyasal reaksiyonlar sonucu değişiyorsa absorbans da değişir. Ortamdaki asitler ve çözgen önemli etkendir.

Cihazdan Kaynaklanan Sebepler: Etkin bant genişliği ebg geniş olan cihazlarda seçimlilik az olacaktır. Çünkü dalga boyu aralığı biraz fazla olacağı için soğurma yapan başka türlerde ölçülmüş olur. Cihazın parçalarından kaynaklanan saçılmalar ve yansımalar dedektöre ulaşırsa yanlış değerler elde edilir.
2.6.) Spektrofotometrik Analizler
Nitel Analizler: Geniş uygulama alanları, yüksek duyarlılık, seçimlilik ve tekrarlanabilirliğin iyi olması, uygulanabilirlik ve hızlılığın iyi olması gibi nedenlerle tercih edilirler.
Nicel Analizlerde: Uygun dalga boyu seçilmeli. Ortamın pH değeri iyi ayarlanmalı. Farklı iki türün molar soğurma katsayılarının aynı olduğu dalga boyu (izobestik nokta) ve her iki türün dengede olduğu pH seçilir.
 Ayrıca reaktif derişimi ve sıcaklıkta önemlidir.
Nicel analizler; tek standartla, kalibrasyon eğrisi ile ve standart katma metodu ile yapılabilir. Kalibrasyon grafiğinde absorbans ile derişim arasında grafik çizilir. Örneğin absorbası grafik denkleminde y değeri yerine konularak derişim (x değeri) bulunur. Veya örneğin absorbansının eğriyi kestiği yerden x eksenin dikme indirilerekte aynı şekilde örneğin derişimi bulunabilir.

2.7.) MOT İLE DALGA BOYU ARASINDAKİ İLİŞKİ
Basit bir serbest-elektron moleküler orbital modeli, poliasetilen gibi lineer zincirli atomlardan yapılan iletken, yarıiletken ya da yalıtkan bir malzemeyi nicel olarak tanımlamak için ihtiyaç duyulan minimum elemanları bize sağlar. d mesafesiyle birbirinden ayrılan N atomlu bir dizi farz edelim. Zincirin toplam uzunluğu (N–1)d veya büyük N için yaklaşık olarak Nd olsun. Bir boyutlu kutudaki (kutunun içinde potansiyel sıfır ve dışında sonsuz) serbest parçacığın, kuantum mekaniksel modele göre, dalga fonksiyonlarına (Şek. 6) aşağıdaki özdeğer serisi karşılık gelir.

(4)

Burada h Planck sabitidir. m elektronun kütlesi ve n kuantum sayısıdır.
Moleküler orbital başına iki elektron olmak üzere (pauli dışarlama prensibine göre), N tane p-orbitalindeki elektronların, bu seriye uygun biçimde, moleküler orbitallere yerleştirildiğini farz edersek, en yüksek dolu orbital (HOMO) aşağıda verilen enerjiye sahip olur.

(5)

En düşük boş moleküler orbitalin enerjisi de aşağıdaki gibi olur.

(6)

Bir elektronu HOMO dan LUMO ya uyarmak için gerekli enerji ise

(7)

olur. Bu bağıntıdan, polimer uzunluğunun artması ile band gapın (1/N ile) azaldığı açıkça görülür ve böylece makroskobik boyutlarda pratik olarak tamamen kalkacaktır.

d)

Şekil 6 Serbest elektron modeli (L uzunluğunda bir boyutlu kutu): (a) Enerji seviyeleri ve (b) dalga fonksiyonları. Belli bir konumda dalga fonksiyonunun karesi, parçacığın bu konumda bulunma olasılığıdır. Model çok elektronlu moleküler orbital tanımına uygulanmıştır: (c) de 16 elektron ilk sekiz moleküler orbitali doldurmuştur. En yüksek dolu molekler orbital HOMO ile belirtilmiştir, sonraki boş olan da LUMO ile gösterilmiştir. (d) de bir elektron HOMO dan LUMO ya yükseltilmiştir (zıt spinli olacak şekilde, S = 0).




Başka modeller de nitel olarak benzer bilgiler verebilir. Bunlar; p elektronlu sistemler için Hückel modeli veya daha gelişmiş yarı-ampirik modeller ve data programları veya ab initio modellerdir (örneğin John Pople’nin Gaussian programları, 1998 Nobel kimya ödülü). Çok elektronlu sistemler için toplam dalga fonksiyonu bir durumu oluşturur (en basit modelde bir elektronlu dalga fonksiyonlarının hepsinin çarpımıdır, örneğin dolu orbitaller) ve onun enerjisi tüm sistemin enerjisidir. Çift sayıda elektronlar durumunda, her iki elektron en düşük enerjili orbitalden başlayarak her bir orbitale yerleştirilir ve böylece taban durumuna karşılık gelen Şek.6 c deki gibi bir yapıya sahip oluruz. Bütün elektronlar çiftlendiğinden toplam spin açısal momentumu S sıfırdır, dolayısıyla madde manyetik değildir.
Eğer dolu moleküler orbitallerin birinden bir elektron, üstte boş moleküler orbitallerden birine taşınırsa (Şek.6 d), uyarılmış bir elektron konfigürasyonu oluşur ve buna karşılık gelen uyarılmış durum taban durumundakinden daha yüksek bir enerjiye sahip olur. Taban durumu ve uyarılmış durum arasındaki minimum enerji farkı (band gap), düşük düzeyde bir pozitif yük ya da “hole” ve üst orbitallerde (boş orbitallerde) de bir elektronlu yük çifti oluşturmak için gerekli enerjiye karşılık gelir. Eğer düşük orbitalde tek kalan elektronun spini ile uyarılmış elektronunki birbirine zıt ise, S yine sıfırdır (S = 1/2 – 1/2 =0) ve uyarılmış durum bir singlet durumdur (manyetik değildir). Hâlbuki iki spin paralel olursa, S = 1/2 + 1/2 = 1 olur ve bu duruma da triplet durum denir (madde paramanyetiktir, yani molekül elektron spininden dolayı sürekli bir manyetik dipol momente sahiptir).
Bizim basit serbest-elektron modelimizde (Denk.7) band gapın yeterince uzun zincir için sıfır olacağını ve bu nedenle de poliasetilenin bir iletken gibi davranabileceğini gördük. Deneysel olarak, band gap maddenin elektronik spektrumundaki birinci absorbsiyon bandının dalga boyu ile orantılıdır. Böylece, enerji şartı yerine getirilirse, l dalga boyuna sahip bir foton, bir elektronu HOMO düzeyinden LUMO ya uyarabilir. Bu şart

(8)

dir. Burada h Planck sabiti ve n ışığın frekansı (n=c/l) ve c de ışığın hızıdır. Bu yüzden, polienler uzunluğu artıkça absorbsiyonun dalga boyu da uzar: Etheneden butadiene, hexatriene doğru çift bağlar ekleyerek daha uzun konjüke moleküller yapıldığında, band gap DE de azalır, fakat Denk.7 ki gibi değil. Böylelikle bir üst limitin varlığı ortaya çıkar ve bu üst limitin dışında yapılacak daha fazla konjügasyondan sonra sonsuz lineer poliene değişim oluşmaz. Bu yakınsama birkaç teorik öngörü ile de teyit edilmiştir. Bunların ilki 1937 de Lennard-Jones tarafından ileri sürülmüştür. Böylece, önemli bir band gap ve dolu valans orbitallerine sahip poliasetilenin bir iletken olması beklenmez. 10–5 – 10–7 civarında kendine özgü (intrinsic) bir iletkenliği ile poliasetilen bir yarıiletkendir. Yarıiletkenlerden beklendiği gibi, elektronların termal uyarılmalarının gerekli bir sonucu olarak, sıcaklık azaldıkça iletkenlik de azalır (T = 0 da sıfırdır). Aksine, metallerin iletkenliği sıcaklık azaldıkça artar.
Aşağıdaki şekilde poliasetilenin optik absorbsiyon spektrumu gösterilmiştir. p ve p* orbitalleri arasındaki HOMO-LUMO gapı 1.7eV civarındadır. Bu değer, yaygın inorganik yarıiletkenler için gözlenilen gap değerine benzerdir. Bunlar: GaAs 1.43eV, Si 1.14eV ve Ge 0.67 eV. Dolayısıyla katkılama mekanizmi, band gap içinde (“aragap: midgap” durumlar), elektronların termal uyarılmayla atlayabileceği lokalize durumların üretilmesiyle, açıklanabilir.

Şekil 7 Katkısız poliasetilenin optik absorbsiyonu (eğri 1). Klasik bir yarıiletken gibi numune, band gapdan (1.7eV) daha düşük foton enerjisine sahip ışık için, saydamdır (transparan). 2 ve 3 eğrileri artan dopant (katkılama maddesi) ile poliasetilenin absorbsiyonunu göstermektedir.



3.) DENEYİN YAPILIŞI

1000 ppm lik bir salisilik asid stok çözeltisinden 5 ppm, 10 ppm, 20 ppm, ve 40 ppm lik çözeltiler hazırlandı. Hazırlanan bu çözeltiler sırayla UV-VIS spektrofotometresine konularak absorbans değerleri ölçüldü ve konsantrasyonlarına karşılık absorbans grafiği çizildi. Çizilen bu grafik yardımıyla konsantrasyonu bilinmeyen salisilik asid çözeltisinin konsantrasyonu tayin edildi.





4.)VERİLER VE HESAPLAMALAR

Grafik.1.Absorbansa karşılık konsantrasyon grafiği

UV-VIS spektrofotmetresinde bilinmeyen çözeltimiz 0,327 abs olarak ölçüldü.

Bu grafikten yararlanarak konsantrasyonu bilinmeyen maddenin konsantrasyonunu ;




buradan

 dir.